Inscribing circles within a circle
- Gemami Junior
- Jun 10, 2020
- 1 min read
Another interesting construction challenge, whether you use pencil and a pair of compasses or geometric drawing software. Neat use of angle bisectors.
Divide circle into 2n sectors (the diagram shows 4 inscribed circles so need 8 sectors). The key to this construction is that the centre of a circle must lie on the angle bisector of its tangents. If one tangent is one of the radius drawn, by drawing a tangent off an adjacent radius and then bisecting the angle between this tangent and an extended radius, the centre of one of the smaller circles can be found. Once one centre is found, the other three must be an equal distance from the original centre, so sing a pair of compasses or otherwise, the other 3 centres can be found
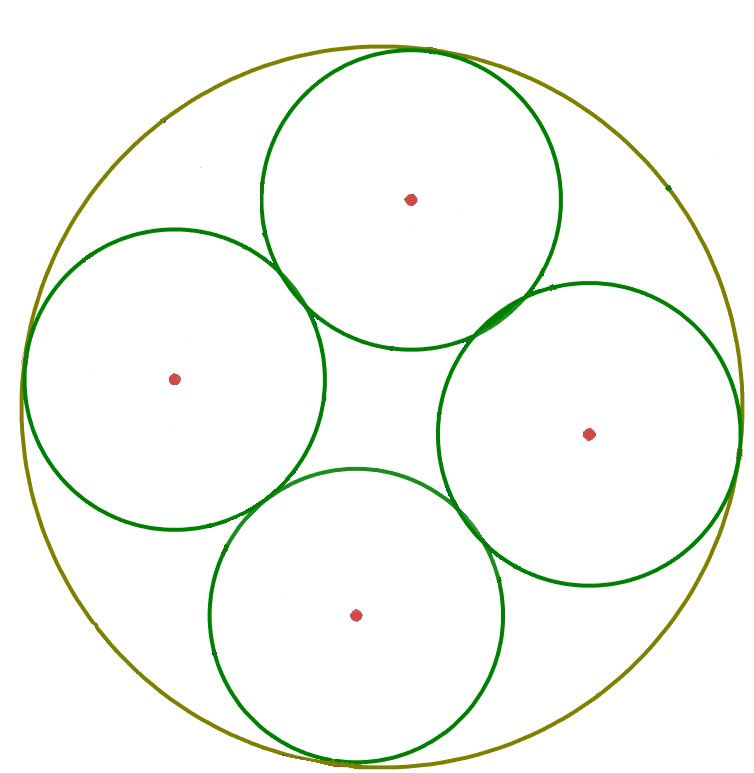
and of course the colour version for those that prefer







Comments